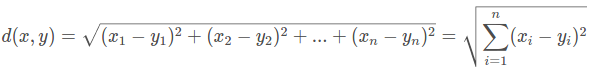KNN和K-means算法

区别

	KNN	K-means
目标	目标是为了确定一个点的分类	目标是为了将一系列点集分成k类
算法类别	分类算法	聚类算法
学习类型	监督学习，类别是已知的，通过对已知分类的数据进行训练和学习，找到这些不同类的特征，再对未分类的数据进行分类	非监督学习，事先不知道数据会分为几类，通过聚类分析将数据聚合成几个群体。聚类不需要对数据进行训练和学习
训练数据集	训练数据集有label，已经是完全正确的数据	训练数据集无label，是杂乱无章的，经过聚类后才变得有点顺序，先无序，后有序
训练过程	没有明显的前期训练过程	有明显的前期训练过程
K值结果	K值确定后每次结果固定	K值确定后每次结果可能不同，从 n个数据对象任意选择 k 个对象作为初始聚类中心，随机性对结果影响较大
时间复杂度	O（n）	O(nkt)，t为迭代次数

K-最近邻算法(KNN)

介绍

K 最近邻（KNN，K-NearestNeighbor）分类算法是数据挖掘分类技术中最简单的方法之一。所谓 K 最近邻，就是 K 个最近的邻居的意思，说的是每个样本都可以用它最接近的 K 个邻近值来代表。 K 最近邻算法就是将数据集合中每一个记录进行分类的方法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。

步骤

对未知类别属性的数据集中的每个点依次执行以下操作:
(1) 计算已知类别数据集中的点与当前点之间的距离;
(2) 按照距离递增次序排序;
(3) 选取与当前点距离最小的k个点;
(4) 确定前k个点所在类别的出现频率;
(5) 返回前k个点出现频率最高的类别作为当前点的预测分类

举一个关于KNN算法的例题

假设有如下 6 个数据点，其中前 5 个为训练数据，分别有两个特征 x1 和 x2。最后一个数据点是测试数据，需要通过 KNN 算法预测其所属类别。

编号	x1	x2	类别
1	1	4	A
2	2	3	A
3	3	6	A
4	4	2	B
5	5	8	B
6	6	7	？

我们现在需要用 KNN 算法对第 6 个数据点进行分类。假设 K=3，即在训练数据中找三个离第六个数据点最近的点，再根据这三个点的分类来判断第六个数据点的类别。

首先，需要用欧氏距离计算每个训练数据点和第六个数据点之间的距离：

编号	x1	x2	类别	距离
1	1	4	A	3.605
2	2	3	A	3.162
3	3	6	A	1.414
4	4	2	B	5.099
5	5	8	B	2.236

然后，将距离从小到大排序，取达到 K 值的前 K 个数据点：

编号	x1	x2	类别	距离
3	3	6	A	1.414
2	2	3	A	3.162
5	5	8	B	2.236

最后，统计前 K 个数据点中类别最多的类别，将该类别作为第六个数据点的预测类别。在这个例子中，前 K 个数据点中 A 的数量为 2，B 的数量为 1，因此第六个数据点被预测为 A 类。

这就是 KNN 算法的基本流程，通过计算距离、排序和统计来判断新数据点的类别。在实际应用中需要根据不同的场景来选择合适的距离度量方法和 K 值，从而来达到最好的分类效果。

代码

代码依据步骤而写，从菜鸟教程上找理解

from math import sqrt
from collections import Counter

# 训练数据集
X_train = [
    [1, 4, 'A'],
    [2, 3, 'A'],
    [3, 6, 'A'],
    [4, 2, 'B'],
    [5, 8, 'B']
]

# 测试数据集
X_test = [6, 7]

# 欧氏距离计算函数
def euclidean_distance(x1, x2):
    distance = 0.0
    for i in range(len(x1)):
        distance += (x1[i] - x2[i]) ** 2
    return sqrt(distance)

# KNN 算法实现函数
def knn(X_train, X_test, k):
    # 保存距离及其类别的列表
    distances = []

    # 遍历训练数据集，计算每个样本与测试数据之间的距离，并保存距离及其类别
    for i in range(len(X_train)):
        dist = euclidean_distance(X_train[i][:2], X_test)
        label = X_train[i][-1]
        distances.append((dist, label))

    # 将距离列表按照距离从小到大排序
    distances.sort()

    # 找出前 K 个距离最近的点
    k_nearest_neighbors = []
    for i in range(k):
        k_nearest_neighbors.append(distances[i][-1])

    # 统计前 K 个点中出现次数最多的类别，即为测试数据的预测类别
    most_common = Counter(k_nearest_neighbors).most_common(1)
    return most_common[0][0]

# 假设 K=3，将测试数据分类
predicted_class = knn(X_train, X_test, k=3)

# 输出预测结果
print("Predicted class for X_test is:", predicted_class)

代码解析：

1.首先定义了训练数据集 X_train 和测试数据集 X_test。
2.定义了一个欧氏距离计算函数 euclidean_distance()，用于计算两个数据点之间的欧氏距离。
3.定义了 KNN 算法实现函数 knn()，其中按照流程先计算所有训练数据点与测试数据之间的距离，然后将距离从小到大排序，并选出前 K 个距离最近的数据点，统计这些数据点中每个类别出现的次数并找到出现次数最多的那个类别，即为测试数据的预测类别。
4.在主程序中调用 knn() 函数，假设 K=3，将测试数据分类，并输出预测结果。

图像代码不过多阐述

K均值算法(K-means)

介绍

聚类算法，将一堆数据划分成到不同的组中。根据样本特征的相似度或距离远近，将其划分成若干个类。

聚类：物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。

簇：本算法中可以理解为，把数据集聚类成 k 类，即 k 个簇。

质心：指各个类别的中心位置，即簇中心。

步骤

从数据中选择k个对象作为初始聚类中心
计算每个聚类对象到聚类中心的距离来划分
再次计算每个聚类中心
计算标准测度函数，直到达到最大迭代次数或者满足收敛条件，则停止，否则，继续2操作

伪代码

复杂度
我们先看下伪代码：

获取数据 n 个 m 维的数据
随机生成 K 个 m 维的点
while(t)
    for(int i=0;i < n;i++)
        for(int j=0;j < k;j++)
            计算点 i 到类 j 的距离
    for(int i=0;i < k;i++)
        1. 找出所有属于自己这一类的所有数据点
        2. 把自己的坐标修改为这些数据点的中心点坐标
end

时间复杂度： $O(tknm)$，其中，t 为迭代次数，k 为簇的数目，n 为样本点数，m 为样本点维度。

空间复杂度： $O(m(n+k))$，其中，k 为簇的数目，m 为样本点维度，n 为样本点数。

优缺点

优点

容易理解，聚类效果不错，虽然是局部最优，但往往局部最优就够了；
处理大数据集的时候，该算法可以保证较好的伸缩性；
当簇近似高斯分布的时候，效果非常不错；
算法复杂度低。

缺点

K 值需要人为设定，不同 K 值得到的结果不一样；
对初始的簇中心敏感，不同选取方式会得到不同结果；
对异常值敏感；
样本只能归为一类，不适合多分类任务；
不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。

举一个关于K-means算法的例题

如果簇的数目k=2，根据下表数据（n=8）行数据，按照k-means算法，写出每次迭代过程以及最终得到簇的数据所在的序号的集合。

序号	属性1	属性2
1	1	1
2	2	1
3	1	2
4	2	2
5	4	3
6	5	3
7	4	4
8	5	4

提示：（1）第一次迭代先随机找两行数据，如第一行和第三行当为初始点。

（2）计算距离，可以用欧式距离（上文提到过）

手写推演

代码

import numpy as np

# 定义 KMeans 算法类
class KMeans:
    def __init__(self, k=2, max_iter=100):
        self.k = k
        self.max_iter = max_iter
    
    # 训练模型函数，将数据集分为 k 个簇，并返回每个数据点所属的簇的序号
    def fit(self, X):
        centroids = X[np.random.choice(len(X), self.k, replace=False)] # 随机选择 k 个数据点作为簇的初始中心
        for i in range(self.max_iter):
            distances = np.sum((X - centroids[:, np.newaxis]) ** 2, axis=2) # 计算每个数据点到各个簇中心的距离
            labels = np.argmin(distances, axis=0) # 将每个数据点归属到距离最近的簇
            new_centroids = np.array([X[labels == j].mean(axis=0) for j in range(self.k)]) # 计算新的簇中心位置
            if np.allclose(new_centroids, centroids): # 如果新中心和旧中心相同，则算法收敛
                break
            centroids = new_centroids # 更新中心
        return labels
    
# 定义数据集
X = np.array([[1, 1], [2, 1], [1, 2], [2, 2], [4, 3], [5, 3], [4, 4], [5, 4]])

# 初始化 KMeans 模型对象，设置 k=2
kmeans = KMeans(k=2)

# 训练模型并输出每个数据点所属的簇的序号
labels = kmeans.fit(X)
print(labels)

代码解析：

1.定义 KMeans 算法类 KMeans，其中包括初始化函数 init() 和训练模型函数 fit()。在 fit() 函数中，首先随机选择 k 个数据点作为初始簇中心，然后迭代若干次，每次计算所有数据点到各个簇中心的距离，将每个数据点归属到距离最近的簇，并计算新的簇中心位置；如果新中心和旧中心相同，则算法收敛，停止迭代。
2.定义数据集 X。
3.初始化 KMeans 模型对象 kmeans，并将 k 值设置为 2。
训练模型并输出每个数据点所属的簇的序号。